Centrifugal effects: the role of curvature in modifying frontal stability and instability

More recently, I led a study which was purely theoretical. We discovered that curvature found within ocean fronts may cause cyclonic fronts to be less stable than anticyclonic fronts at low Richardson numbers (\(Ri \sim 1\)). This goes against our present understanding of stability/instability since under geostrophic flow at \(Ri = 1\), stable flow requires all vorticity to be cyclonic. That is, \(Ro > 0\). This change in the threshold for stability/instability can also help to explain why most submesoscale coherent vortices are anticyclonic. My coauthors and I have since written a two-part paper on the subject (part 1 & part 2). Additionally, I have developed arguments for a new form of potential vorticity valid on small horizontal scales.

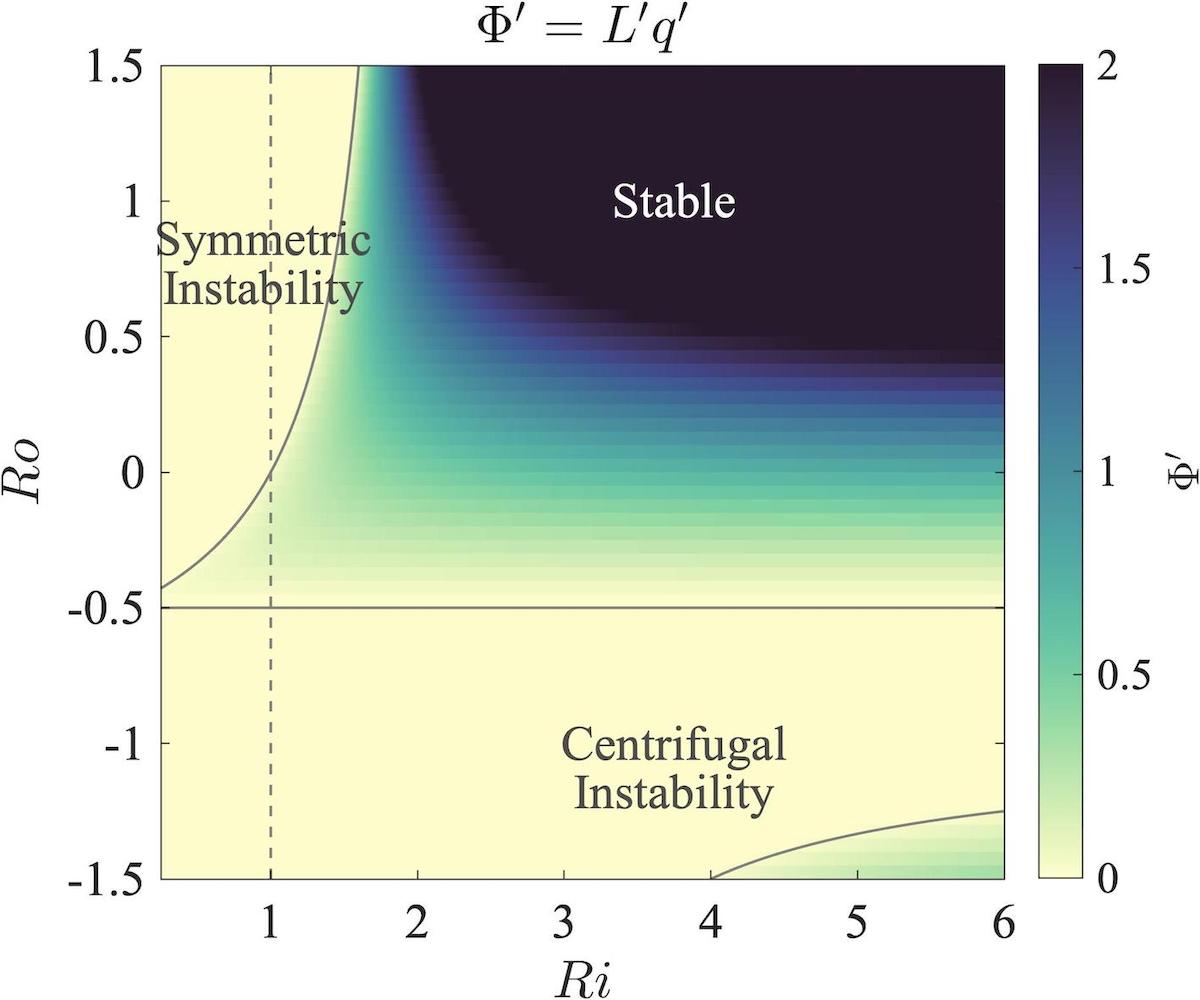
The figure below illustrates stable and unstable regimes within a curved front given a curvature-to-vorticity ratio of \(\mu = 2\). This is characteristic, for instance, of a Gaussian vortex at the radius of maximum velocity \(r_{m}\). The \(x\) axis is the gradient Richardson number \(Ri\) and \(y\) axis is the gradient Rossby number \(Ro = \zeta/f\), where \(\zeta\) is vorticity and \(f = 2\Omega\sin{\theta}\) is the Coriolis parameter. One sees that at low Richardson numbers, flow can be strongly unstable for cyclonic motion while weakly stable for anticyclonic motion. This may help to explain the elevated numbers of submesoscale anticyclones versus submesoscale cyclones in the vorticity record, for which \(Ro\) is appreciable and \(Ri\) is typically small. It also may have implications for parcel motion within highly curved fronts and, thus, vertical tracer flux within the upper ocean. In this graphic, the horizontal line at \(Ro = 0.5\) corresponds to the threshold for centrifugal instability, while the curved line corresponds to the threshold for symmetric instability.

Background theory

For a fluid parcel in cyclogeostrophic and hydrostatic balance (i.e. gradient wind balance), the regions of stability and instability are determined by the sign of the discriminant, \(Lq\), where \(L = rv + fr^2/2\) is the absolute angular momentum and \(q = \omega_{a} \cdot \nabla b\) is the Ertel PV. (Here, \(v\) is the azimuthal velocity at radius \(r\).) For stable stratification away from the Equator, this can be rewritten in a non-dimensional form: \(\Phi' = L'q' = (1 + Cu)(1 + Ro) - (1 + Cu)^2 Ri^{-1}\), where \({L' = 1 + Cu}\) is a non-dimensional form of absolute angular momentum, \(Cu = 2v/(fr)\) is a non-dimensional number quantifying the curvature of the flow, and \(q'\) is a non-dimensional form of Ertel PV. Essentially, \(L'\) quantifies the effect of centrifugal forces, while \(q'\) quantifies the effect of both stratification and shear on the stability of fluid parcels.