My research seeks to understand small-scale dynamics that potentially have climate-scale impacts. Specifically, I seek to better understand mesoscale and submesoscale processes in the ocean and their impact on turbulence and mixing in the ocean. Mesoscale currents can be broadly classified as having horizontal scales of 50-200 km, vertical scales of 0.5-1 km, and evolving on time scales of 10-30 days. In contrast, submesoscale currents are often classified as having scales much smaller than these: 1-30 km in the horizontal, 10-200 m in the vertical, and evolving over hours to days. Examples of phenomena common to both include ocean surface fronts, deep boundary flows, and vortices. However, because the intensity of submesoscale currents are an order of magnitude greater, submesoscale phenomena have the ability to generate turbulence and mixing, with potential impacts on global ocean circulation.

More recently, I led a study which was purely theoretical. We discovered that curvature found within ocean fronts may cause cyclonic fronts to be less stable than anticyclonic fronts at low Richardson numbers (\(Ri \sim 1\)). This goes against our present understanding of stability/instability since under geostrophic flow at \(Ri = 1\), stable flow requires all vorticity to be cyclonic. That is, \(Ro > 0\). This change in the threshold for stability/instability can also help to explain why most submesoscale coherent vortices are anticyclonic. My coauthors and I have since written a two-part paper on the subject (part 1 & part 2). Additionally, I have developed arguments for a new form of potential vorticity valid on small horizontal scales.

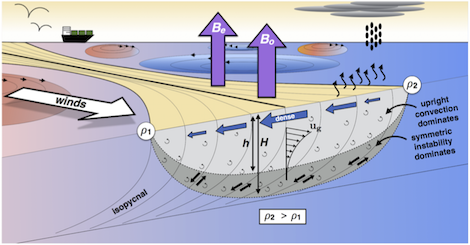
Submesoscale processes occurring within the upper ocean have attracted considerable attention within the past 15-20 years. This has likely been prompted by an increase in spatial and temporal resolution within (a) numerical simulations of the ocean and (b) ocean observations. The former can be attributed to increased computational capability, while the latter has almost certainly resulted from autonomous technological developments (e.g., ocean gliders, SailDrone, float technology). Dynamically, these small-scale processes are expected to have implications for biogeochemistry (e.g. carbon exchange) and ocean circulation. Submesoscale processes in the ocean include but are not limited to the following: (1) baroclinic instability and (2) symmetric instability. My coauthors and I have examined both processes. However, for brevity, the second of these instabilities is detailed below.

The oceans are turbulent and chaotic. Described by simple analytical equations at mesoscales or larger, these two-dimensional flows have a unique behavior: eddying processes interact with one another in a non-linear manner to create larger and larger vortices. One refers to this as an inverse energy cascade. For example, within a tank with constant rotation rate, \(\Omega = f / 2\), an in the absence of friction, these vortices would coalesce until a single vortex would remain. However, on a rotating sphere such as Earth where \(f\) varies with latitude, there exists a theoretical constraint placed on the north-south extent of eddies. Oddly, this constraint is not present in the zonal extent. This dynamic—referred to as a forward enstrophy cascade—is thought to result in locations of pronounced horizontal shear, or multiple zonal jets. Additionally, the conservation of enstrophy (squared vorticity) plays an important role. It is notable that these arguments have been used to explain banded structures on Jupiter.